ーーーーーーーー
主要内容
ーーーーーーーー
昔、統計検定2級に合格したんですが、だいぶ忘れてます。統計学入門的な内容から勉強し直してます。
正規分布や標準正規分布の図はおなじみの物だと思いますが、縦軸を省略しているものが多く、そういや縦軸を省略せずに表すとするとどんな表記になるんだろ?と思ってたことがあります。自分の備忘録として記載したいと思います。
表題について解決に導いてくれた3冊の書籍を紹介させていただきます。
↓↓↓
紹介書籍
紹介書籍①:
【リンク】⇒Amazon/通販/商品紹介ページ;大村 平(改訂版2002年) 『統計のはなし-基礎・応用・娯楽-【改訂版】』 株式会社日科技連出版社
紹介書籍②:
【リンク】⇒Amazon/通販/商品紹介ページ;東京大学教養学部統計学教室(編)(1991年) 『統計学 基礎統計学Ⅰ』 一般財団法人東京大学出版会
紹介書籍③:
【リンク】⇒Amazon/通販/商品紹介ページ;日本統計学会(編)(2013年) 『日本統計学会公式認定 統計検定1級対応 統計学』 東京図書株式会社
↓↓↓
紹介書籍①では、正規分布や標準正規分布の縦軸をyとして解説してくださっているページがあります。(因みに、正規分布の横軸はx、標準正規分布の横軸はZです。)
紹介書籍②では、正規分布の縦軸をf(x)として表記しています。
紹介書籍③では、正規分布に限らず確率密度関数の縦軸をfx(x)として表記しています。
紹介書籍①~③より学んだ正規分布と標準正規分布の関数を記載しておきます。
「正規分布」・・・連続型確率変数を持つ確率分布の一つ。英語ではnormal distributionであり、「ありふれた分布」とか「通常の分布」という雰囲気なのだそう。
「確率密度関数」・・・連続型確率変数を持つ確率分布の曲線自体を表す関数。
「累積分布関数(分布関数)」・・・連続型確率変数を持つ確率分布曲線下の面積を表す関数。つまり、「確率密度関数」を積分している形となっている。
「標準正規分布」・・・標準化された正規分布。英語ではstandard normal distribution。
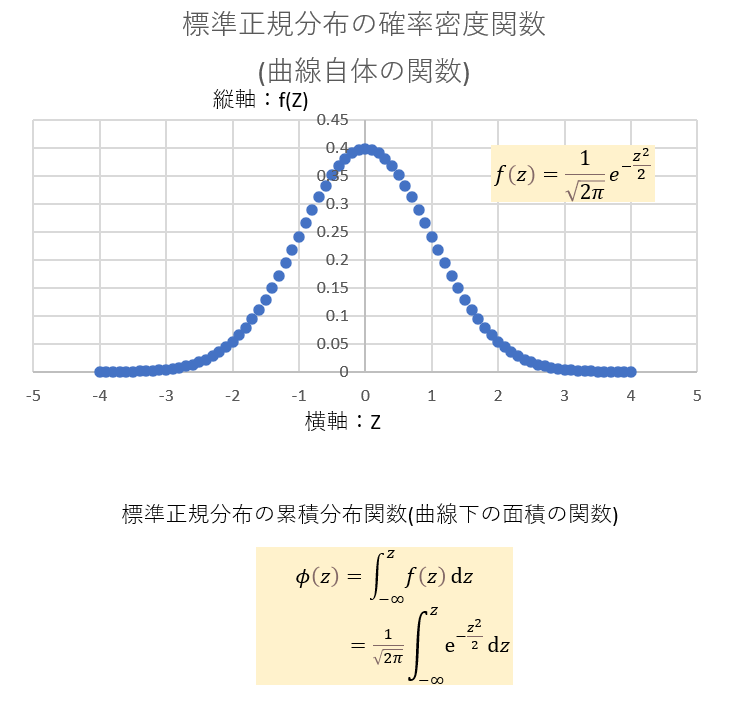
正規分布や標準正規分布の縦軸
これは、そのxという事象が起こる度数みたいなものだと思います。
曲線下面積は、ご存知「確率」を表しています。
数式は下の2つの図に書き込みました。
〖追記①:2021/9/1追記
正規分布f(x)におけるxのときの縦軸はxという事象の相対度数、標準正規分布f(Z)における標準化変数Zのときの縦軸は、xという事象に対応する標準化変数Zの相対度数と思っています。※明示されている資料がまだ見つかっていないので、これは今後確認が必要です。
正規分布のf(x)の曲線下面積の総面積を1にするため、に「1/σ(2π)^(1/2)」という係数をネイピア数の累乗項に掛けているのだそうです。正規分布でも標準正規分布でも曲線下面積は確率を表しており、それぞれその総面積が1です。よって、正規分布f(x)におけるxのときの縦軸はxという事象の相対度数、標準正規分布f(Z)における標準化変数Zのときの縦軸は、xという事象に対応する標準化変数Zの相対度数なのではないかと思っています。
〗
〖追記②:2021/9/3追記
ネットサーフィンしていたら「確率密度」という語があることを知りました。ほへ~!関数名は「確率密度関数」なので「確率密度」の関数ですよ、ということなのですね、きっと。リンクを貼るべきなのかちょっと分からずに記載してしまい大変恐縮なのですが、そのサイトさんによると、「確率密度」とは「相対的な出やすさ」なのだそうです。おお!ということは、私の2021/9/1の追加訂正で記載した「縦軸は『相対度数』」は当たらずしも遠からず、という感じでしょうか?(←違うかf(^^;))
相対的な出やすさ、ということは「相対的な確率」という感じなのでしょうかねえ。「相対度数」は「相対的な事象の数」だから「相対的確率」とは異なるものですが、似ているイメージを持ってしまいます、わたくし。とりあえず「相対」というところまではばっちり合ってた、ということで大目にみていただけないものでしょうか(><)。(←もちろん、厳密にはダメ~!!)
今回の情報源はネットサーフィンなので、今後、明示されている書籍などの資料が見つかったら追記したいと思います。(`・ω・´)ゞ
〗

( ↑ 正規分布の曲線下面積については、これを累積分布関数として定義している書籍を今のところみかけてないので、このような表記としました。)
↓↓↓
備忘録としてですが、ブログにまとめていると、自分の学習・復習・勉強にも良いような気がしました。
('◇')ゞ
(#^^#)