ーーーーーーーー
主要内容
ーーーーーーーー
昔、統計検定2級に受かりましたが、「自分、統計検定2級です」と堂々と言えないくらいにいろいろ忘れとる感じです(汗)。統計学入門的な内容をいろいろ復習しながら、備忘録として記事にしていきたいと思います。
以下に、参考にした書籍を4つ紹介しておきますね。
〖2021/2/19 追記;紹介書籍をもう一つ追記しておきます〗
↓↓↓
紹介書籍
紹介書籍①:
【リンク】⇒Amazon/通販/商品紹介ページ;東京大学教養学部統計学教室(編)(1991年) 『統計学 基礎統計学Ⅰ』 一般財団法人東京大学出版会
紹介書籍②:
【リンク】⇒Amazon/通販/商品紹介ページ;栗原伸一 (2011年) 『入門 統計学 -検定から多変量解析・実験計画法まで-』 株式会社オーム社
紹介書籍③:
【リンク】⇒Amazon/通販/商品紹介ページ;栗原伸一・丸山敦史(共著)/ジーグレイプ(制作)(2017年) 『統計学図鑑』 株式会社オーム社
紹介書籍④:
【リンク】⇒Amazon/通販/商品紹介ページ;涌井良幸・涌井貞美(2015年) 『まなびのずかん 統計学の図鑑』 技術評論社
〖2021/2/19 追記;紹介書籍をもう一つ追記しておきます
紹介書籍⑤:
【リンク】⇒Amazon/通販/商品紹介ページ;日本統計学会(編)(2015年) 『改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎』 東京図書株式会社
↓↓↓
今回の自分の復習内容は、
母比率の区間推定
です。数式を復習します。検定試験の時に数式を覚えておいて解いた、という記憶があります。ただ、「母比率」って、そもそも何だったっけ?というのもあるので、そこらへんも含めて復習しますです。
記号・数式の表記ルールは、別途まとめている記事のリンクを貼っておきたいと思います。
↓
ではまず、
「母比率」の定義
から行きたいと思います。前述の各紹介書籍での表現を見てみました。
紹介書籍①によると、「母集団の比率」です。
紹介書籍②によると、「母集団において、ある事象が起こる確率」です。
紹介書籍③には(私が見つけられてないだけかもしれませんが)特に記載はないです。ただ、「標本比率」については記載があり、「ある性質を持つ要素の数を標本の全要素数で割った値」というような感じです。この表現を母集団に当てはめて自分で変換してみると、「ある性質を持つ要素の数を母集団の全要素数で割った値」ということになるんだろうなあ、というところです。この予測は次の紹介書籍④での表現を見ると、当たってそうだなあ、と思います。
紹介書籍④によると、「母集団の中でのある事象の割合」みたいな表現です。また、「ある事象の数を母集団の大きさで割った値」みたいな表現です。こちらでは「標本比率」についても記載があり、「ある事象の数を標本の大きさで割った値」というような表現ですので、先ほどの紹介書籍③での自分の予測は当たってそうです。
書籍によって、「母比率」と「標本比率」を表す記号が違っています。
「母比率」  に対して「標本比率」
に対して「標本比率」  (ピーハット)や
(ピーハット)や  (ピーバー)だったり、「母比率」
(ピーバー)だったり、「母比率」  (大文字のアール、ラージアール)に対して「標本比率」
(大文字のアール、ラージアール)に対して「標本比率」  (小文字のアール、スモールアール)だったりします。
(小文字のアール、スモールアール)だったりします。
とりあえずこの記事では、「母比率」  に対して「標本比率」
に対して「標本比率」  (ピーハット)を用いたいと思います。
(ピーハット)を用いたいと思います。
では、
母比率や標本比率の従う分布
についてです。前述のどの紹介書籍でも、標本の大きさ・標本サイズであるnが大きいとき、正規分布に基づいて計算しています。nが大きいときというのは、書籍によってn>30だったりn≧100だったりです。
母比率や標本比率の従う分布に関しては紹介書籍①がとても参考になりました。
まず、前述の正規分布の話を一旦置いておいて、母比率  は二項分布(binomial distribution)に従うのだそうです。
は二項分布(binomial distribution)に従うのだそうです。
↓
二項分布について簡単にいうと、n回繰り返すベルヌーイ試行において、「求める結果」が出る回数が二項分布の確率変数  をとる分布なのだそうです。ということは、とびとびの値をとるということであり、つまりは確率変数
をとる分布なのだそうです。ということは、とびとびの値をとるということであり、つまりは確率変数  は離散型(discrete type)。ということは、二項分布は「散型の確率分布」(p. d. of discrete type ; probability distribution)。
は離散型(discrete type)。ということは、二項分布は「散型の確率分布」(p. d. of discrete type ; probability distribution)。
↓
ベルヌーイ試行(Bernoulli trials)について簡単に言うと、二項試行ともいうらしく、とある試行の結果が「求める結果」と「求めない結果」という2種類しかない試行の事だそうです。n回のベルヌーイ試行において、毎回の試行は前回の試行の影響を受けない、つまり毎回の試行は独立であり、毎回の試行で「求める結果」の出るの確率 は  であり、「求めない結果」の確率は
であり、「求めない結果」の確率は  だそうです。n回繰り返すベルヌーイ試行、つまり二項分布は
だそうです。n回繰り返すベルヌーイ試行、つまり二項分布は  で表しますが、
で表しますが、 を特にベルヌーイ分布(Bernoulli distribution)というのだそうです。
を特にベルヌーイ分布(Bernoulli distribution)というのだそうです。
↓
二項分布について、確率変数  の確率関数は、
の確率関数は、
 ,
,  (
( )
)
ここにおいて、 は二項係数というのだそう。二項分布の確率関数は二項定理より、
は二項係数というのだそう。二項分布の確率関数は二項定理より、
 (ただし、
(ただし、 )
)
と、全確率が1。(なので確率分布だと分かります。)
二項分布の確率変数  の期待値(平均)は
の期待値(平均)は  であり、分散は
であり、分散は  です。
です。
↓
そして、nが大きいとき、という話が出てきます。nが大きいとき、中心極限定理により、離散型確率分布である  は、連続型確率分布である正規分布に近似することができる、となるそうです。
は、連続型確率分布である正規分布に近似することができる、となるそうです。
↓
中心極限定理(Central limit theorem)の概略を示すと、「和  の確率分布の形は、母集団分布が何であっても、nが大きいときには正規分布に近似できる」というものです。母集団分布の平均(母平均)を
の確率分布の形は、母集団分布が何であっても、nが大きいときには正規分布に近似できる」というものです。母集団分布の平均(母平均)を  、分散(母分散)を
、分散(母分散)を  とすると、母集団分布が何であっても、標本の大きさnが大きいとき、「求める結果」が出る回数の和
とすると、母集団分布が何であっても、標本の大きさnが大きいとき、「求める結果」が出る回数の和  について、
について、
 は、正規分布
は、正規分布  に従うと考えて良いそうです。
に従うと考えて良いそうです。
因みに、母集団分布の平均(母平均)を  、分散(母分散)を
、分散(母分散)を  とすると、母集団分布が何であっても、標本の大きさnが大きいとき、確率変数
とすると、母集団分布が何であっても、標本の大きさnが大きいとき、確率変数  の平均
の平均  について、
について、
 は、正規分布
は、正規分布  に従うと考えて良いそうです。
に従うと考えて良いそうです。
↓
ここにきて、やっと正規分布の話になりましたね。(ふう(;´・ω・)。ちょっと一息。)
\(゜ロ\)(/ロ゜)/ \(゜ロ\)(/ロ゜)/ \(゜ロ\)(/ロ゜)/
\(^o^)/
↓
二項分布(n回のベルヌーイ試行)における「求める結果」の回数  は、ベルヌーイ試行
は、ベルヌーイ試行  に従う確率変数
に従う確率変数  の和となるので、
の和となるので、
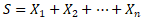
となります。中心極限定理により、これは標本の大きさnが大きいとき正規分布に従うと考えて良いので、二項分布(n回のベルヌーイ試行)における「求める結果」の回数  についての正規分布の標準化変数
についての正規分布の標準化変数  は、二項分布の確率変数
は、二項分布の確率変数  の期待値(平均)は
の期待値(平均)は  であり、分散は
であり、分散は  より、
より、
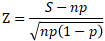
となり、これは標本の大きさnが大きいとき標準正規分布  に近似できます。ここで、n中の
に近似できます。ここで、n中の  の比率は相対頻度(相対度数)ともいえるし、確率変数
の比率は相対頻度(相対度数)ともいえるし、確率変数  の平均
の平均  にであるともいえるみたいです。これが「標本比率」
にであるともいえるみたいです。これが「標本比率」  であり、
であり、
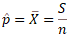
ということみたいです。よって、二項分布(n回のベルヌーイ試行)における「求める結果」の回数  についての正規分布の標準化変数
についての正規分布の標準化変数  を変形すると、
を変形すると、
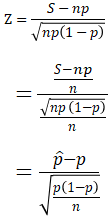
となります。
ようし!やっと、
母比率の区間推定
の数式についてになります。
標本の大きさnが大きいとき、「母比率」  に関する標準化変数
に関する標準化変数  は「標本比率」
は「標本比率」  を用いて
を用いて
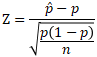
となります。この標準化変数  は標準正規分布
は標準正規分布  に近似的に従うので、
に近似的に従うので、
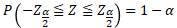
↓
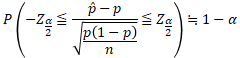
↓
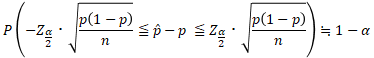
↓
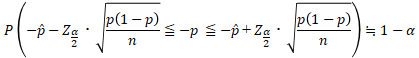
↓
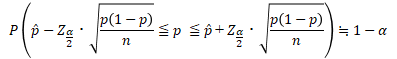
大数の法則(たいすうのほうそく)という「大きな標本で観測された標本平均は母集団の真の平均である母平均とみなしてよい」という法則ですが、この法則により、「標本比率」  は「母比率」
は「母比率」  の一致推定量となるので、nが大きいときは「標本比率」
の一致推定量となるので、nが大きいときは「標本比率」  はほとんど「母比率」
はほとんど「母比率」  に等しいと考えられます。よって、
に等しいと考えられます。よって、
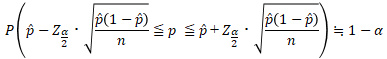
↓
よって、母比率  の信頼係数1-αの信頼区間は近似的に、
の信頼係数1-αの信頼区間は近似的に、
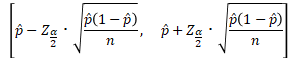
(下のように書くこともあります)
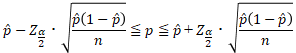
αとZ値を具体的数値にした例を以下に示します。
95%信頼区間ならα=0.5なので  。よって、
。よって、
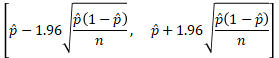
90%信頼区間ならα=0.1なので  。よって、
。よって、
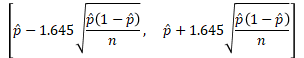
以上の方法は、標本の大きさnが大きいときの「母比率」  の区間推定です。これはWaldというアメリカの統計学者の方が考案したものだそうです。
の区間推定です。これはWaldというアメリカの統計学者の方が考案したものだそうです。
標本の大きさnが小さいときの「母比率」  の区間推定については、AgrestiとCoullという統計学者が考案した数式があるそうで、前述の紹介書籍②及び③にちょっとだけ記載がありましたが、割愛させていただきますね。
の区間推定については、AgrestiとCoullという統計学者が考案した数式があるそうで、前述の紹介書籍②及び③にちょっとだけ記載がありましたが、割愛させていただきますね。
〖2021/2/19 追記;本記事では、「求める結果」が出る回数である確率変数  は二項分布に従い、nが大きいときには中心極限定理により、確率変数の平均
は二項分布に従い、nが大きいときには中心極限定理により、確率変数の平均  に当たる「標本比率」
に当たる「標本比率」  である
である
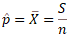
を用いた標準化変数  である
である
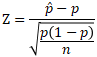
が近似的に正規分布に従い、「母比率」  の区間推定の数式をそこから導く記事を記載しました。
の区間推定の数式をそこから導く記事を記載しました。
紹介書籍⑤では、「(要約):有限母集団において、母集団の大きさNが小さいときの非復元抽出の場合、「求める結果」が出る回数である確率変数  は超幾何分布に従う。Nがある程度大きければ、「求める結果」が出る回数である確率変数
は超幾何分布に従う。Nがある程度大きければ、「求める結果」が出る回数である確率変数  は二項分布に従う。」とあります。そしてそこから標本の大きさnが大きいときに、中心極限定理により・・・と本記事の内容の話と同様に「母比率」
は二項分布に従う。」とあります。そしてそこから標本の大きさnが大きいときに、中心極限定理により・・・と本記事の内容の話と同様に「母比率」  の区間推定の数式の事が記載されていました。さらに、有限母集団と無限母集団の違いについて少し記載されていました~。おお~!\(^^)/〗
の区間推定の数式の事が記載されていました。さらに、有限母集団と無限母集団の違いについて少し記載されていました~。おお~!\(^^)/〗
↓↓↓
区間推定の数式はなんとく覚えてましたが、これを導く過程については記事を書くことによって理解できたような気がします。わ~い!
(*^-^*)
では~!
(^O^)/