ーーーーーーーー
主要内容
ーーーーーーーー
昔、統計検定2級に合格したんですが、だいぶ忘れてますね。統計学入門的な内容から勉強し直してます。
「標準偏差」「標準誤差」「標本誤差」がごっちゃになるので、自分の頭を整理し、備忘録として記事にしますね。
勉強に使用した書籍を下に紹介します。
↓↓↓
紹介書籍
【リンク】⇒Amazon/通販/商品紹介ページ;栗原伸一 (2011年) 『入門 統計学 -検定から多変量解析・実験計画法まで-』 株式会社オーム社
↓↓↓
表題に関して今の私が分かっていることと分かっていないことを明記しておきたいと思います。
分かってないことは【】で括っておきます。
〖2021/2/20 追記;【】で括っておいた疑問点①~⑥について。
疑問点①は、一旦、合っているとしたいと思います。
疑問点②~⑥については、2021/2/20に記載した下の記事をまとめることにより解決しました。
↓
www.my-iroiro-my-tsurezure.jp
〗
用語の表(その1)及び(その2)の修正版
〖2021/8/31 追記;
表「本記事のまとめ表(その1):母集団と標本」及び「本記事のまとめ表(その2):標本誤差」の修正版を載せます。
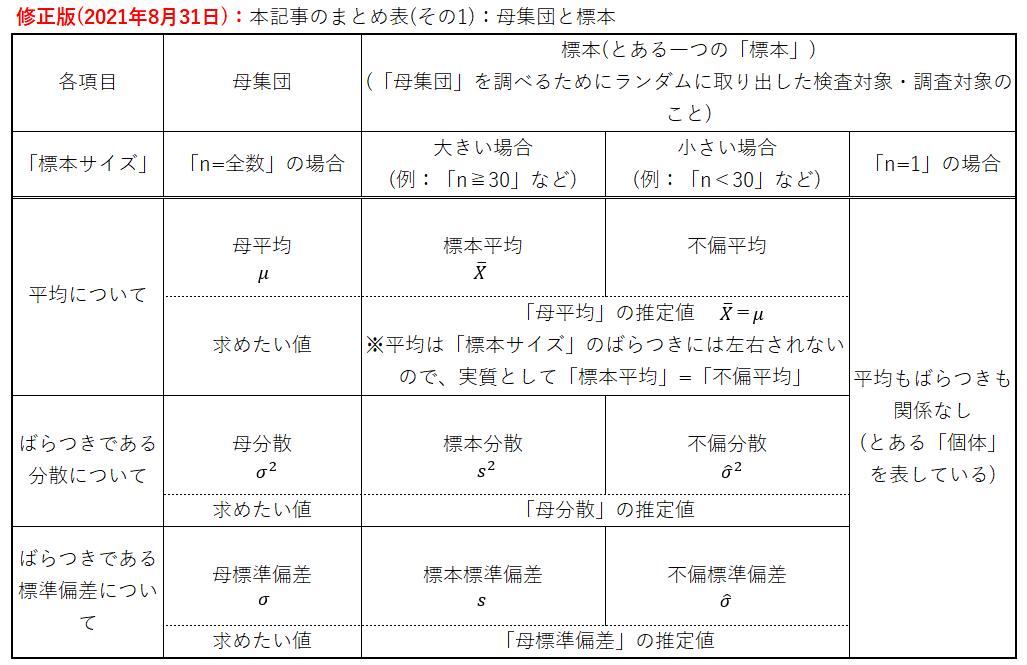

※括弧[ ]の中は私の推測です。
〗
〖2021/8/31 追記;下の2つの表の修正版を上に示しました〗
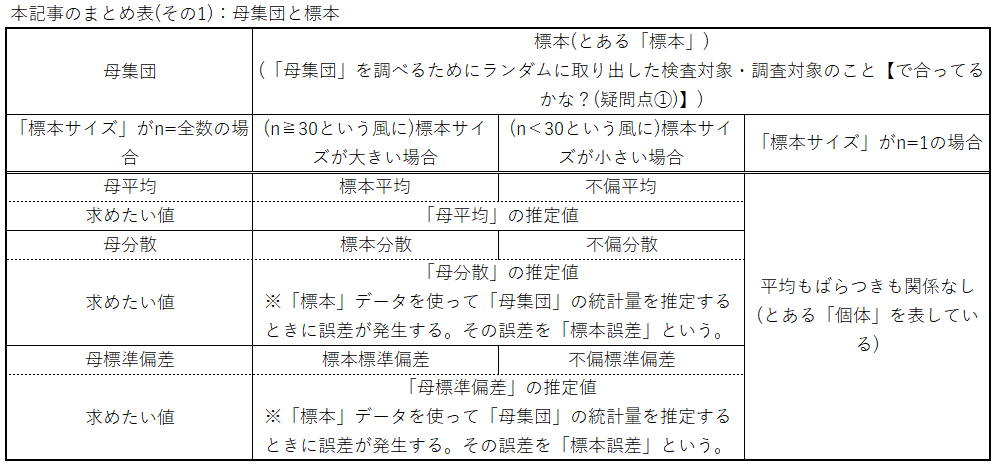

「母集団」・・・調べたい対象のこと
「母平均」・・・「母集団」の平均
「母分散」・・・「母集団」の分散
「標本」・・・「母集団」を調べるためにランダムに取り出した検査対象・調査対象のこと【で合ってるかな?(疑問点①)】
「標本サイズ」・・・とある「標本」の大きさ(いわゆるn数)
「標本平均」・・・とある「標本」の平均(検査・調査における観測値。「標本サイズ」が大きい「標本」の平均は「母平均」の推定値となりうる。)
「標本分散」・・・とある「標本」の分散(検査・調査における観測値。「標本サイズ」が大きい「標本」の分散は「母分散」の推定値となりうる。)
「標本標準偏差」・・・とある「標本」の標準偏差(検査・調査における観測値。「標本サイズ」が大きい「標本」の標準偏差は「母標準偏差」の推定値となりうる。)
「不偏平均」・・・「標本サイズ」が小さい「標本」の平均。小さい「標本サイズ」の「標本」から「母平均」を推定した値。だが、平均は「標本サイズ」のばらつきには左右されないので、実質として「標本平均」=「不偏平均」。
「不偏分散」・・・「標本サイズ」が小さい「標本」の分散。小さい「標本サイズ」の「標本」から「母分散」を推定した値。
「不偏標準偏差」・・・「標本サイズ」が小さい「標本」の標準偏差。小さい「標本サイズ」の「標本」から「母標準偏差」を推定した値。
「標本誤差」・・・「標本平均」から「母平均」を推定するときなど、「標本」データを使って「母集団」の統計量を推定するときに発生する誤差
「標本数」・・・「標本」の数
「標本分布」・・・複数ある「標本平均」の分布【とある「標本」の分布を、複数ある「標本平均」の分布とみなすってこと?(疑問点②)】
「標本平均の平均」・・・【というのがあるということで良いのか?(疑問点③)】
「標本誤差分散」・・・「(複数ある)標本平均の分散(n≧30という風に標本サイズが大きい場合の概念)」【つまり、とある一つの「標本」データから「母集団」を推定する際のその誤差は、標本が複数ある場合とみなしたときのその分散がそれに当たる、ということ?そしてそれが「標本誤差」ってこと?(疑問点④)】
「母誤差分散」・・・「(複数ある)標本平均の分散(母分散が既に分かっている場合の概念)」
「誤差分散」・・・「標本誤差分散」や「母誤差分散」のこと。【これも「標本誤差」を表すものの一つということで合ってる?(疑問点⑤)】
「標本標準誤差」・・・「(複数ある)標本平均の標準偏差(n≧30という風に標本サイズが大きい場合の概念)」【つまり、とある一つの「標本」データから「母集団」を推定する際のその誤差は、標本が複数ある場合とみなしたときのその標準偏差がそれに当たる、ということ?そしてそれが「標本誤差」ってこと?(疑問点⑥)】
「母標準誤差」・・・「(複数ある)標本平均の標準偏差(母分散が既に分かっている場合の概念)」
「標準誤差」・・・「標本標準誤差」や「母標準誤差」のこと。「標本誤差」の大きさを表すものの一つ。
「不偏誤差分散」・・・「(n<30という風に)標本サイズが小さい場合の誤差分散」
「不偏標準誤差」・・・「(n<30という風に)標本サイズが小さい場合の標準誤差」
〈誤差という概念がない場合とは〉
その1:
「標本サイズ」がn=1のとき。これは一個体を表しているので、平均もばらつきも関係なしなのだそう。「標本サイズ」がn=1という「標本」が複数有って分布を作っても「平均の分布」ではなく、「個体別の度数分布」ということになるのだそう。
その2:
「標本サイズ」がn=全数のとき。平均は出るけどばらつきは関係なしなのだそう。「標本サイズ」がn=全数という「標本」をいくら複数作っても平均の値はひとつしかないので、ばらつきなんて発生しない、ということなんだと思う。
↓↓↓
今回の記事では疑問点が①~⑥ありました。
なんか分かったら、都度追記しようかと思ってます。
( =^ω^)